研究平方数表格了解平方数之间的联系
缅华网 伊江树报导
1到100以内的自然数们的平方数表格:
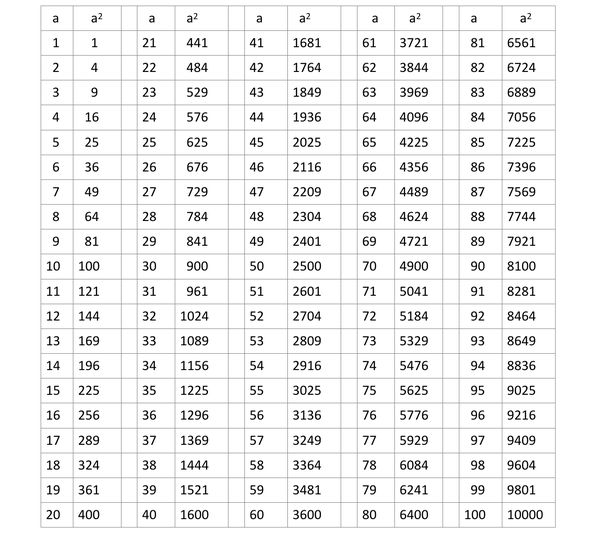
在让老师们填了有关平方数表格后,来开办培训班的数学老师在检查了一下大家所填写的表格,发现没多大差错,第二天就将表格还给老师们,然后就让大家拿着这表格,探讨一下这些平方数的变化情况。
老师们一时都还看不出什么特殊情况。
负责培训班开办工作的数学老师望向了我。
我知道其是想让我先说一说我的发现或感想,当下也就当仁不让,拿起自己手中 的平方数表格,站起来向大家介绍说:
“大家可以先看看50这个平方数,它的平方是2500,这大家都知道,不必多说。现在朝上一格看49的平方数,再抄下一格看51的平方数,有什么发现?”
老师们马上就发现了特点:49的平方是2401,51的平方是2601。
老师们议论纷纷,有的说:“这两个自然数的尾数(最后两位数相同),都是01。”也有的说:“这两个数的平方数十分相似,相差是200。”等等。
“那么再往上一格看48的平方数,往下一格看52的平方数,有什么发现?”
这两个自然数的平方数尾数都是04,两个平方数相差400。
“不必多说了,大家可以接着检查,47与53,46与54,44与56,43与57,42与58,41与59这些自然数的平方数性质了。”
这几组自然数的平方数尾数都相同,而平方数们之间的差别分别是600、800、1200、
1400、1600及1800了。
“表格的其他地方还有类似的情况吗?大家可以找找看。”我说好就坐下来了。虽然我知道在哪里还可以找到这平方数尾数相同的自然数,但不直接说出,让大家自己寻找,可以让大家留下更深刻的印象。
“找到了,在25这个数的附近,各自然数的平方数都有尾数相同的现象。”一位年轻的女老师首先喊叫道。由于是自己寻找发现的,其显得更加兴奋和自豪。
“你是怎样想到会在这里找到这平方数尾数相同的现象?”我笑着问她。
“虽然是靠猜的,”年轻的女老师显然有些不好意思,“但我想,50是这100个自然数的中间数,那么25也是50个自然数的中间数,在这里说不定也会有这种现象,所以找了一下,果然发现真的有这种现象。”
“那么在其他地方还会不会有这种现象呢?”我继续问道。
“那么可能就在75这个数的周围了。”该女孩子说完,就准备在其的平方数表格上寻找之时,已有好几位老师同时叫起来了:
“对!对!在75这个数的周围确实也有这种平方数尾数相同的现象!”
发现了这种尾数相同的地方,老师们都非常兴奋。这时培训班负责老师就给大家布置了一个作业,将平方数尾数相同的自然数都一个一个列出来,看有什么特殊现象。然后再想想看为什么会出现这种尾数相同的现象。
“平方数尾数好像都有一定的规则,不是每一个两位数都会是平方数的尾数,例如11,12,13,14这些数都不会是这些平方数的尾数。”有一位老师这样说道。
“不说两位数,只说个位数的话,我发现只有1,4,5,6,9,0这六个数能成为平方数的尾数,2,3,7,8这四个数完全不能成为这平方数的尾数。”
“那么你们就顺便查一下吧,看哪一些两位数可以作为平方数的尾数出现,有什么发现,我们下一堂颗再讨论。”培训班负责老师这样交代道。
“平方数中,有些数好像也很特别,像169,196及961,1,6,9这三个数倒来倒去,可组成3个不同的平方数,不知还有其他什么数有类似的性质呢?”
“这些大家有兴趣的话,可以顺便整理列出来,大家一起来分析讨论。”
评论列表 共有 0 条评论
最新导读

热门文章















发表评论 取消回复