研究尾数相同的平方数表格
缅华网 伊江树报导
那一天在培训班课堂上,大家讨论到了平方数尾数相同的问题。为了更好地探索这个课题,由学员当中挑选出了4位学员老师,负责检查整理尾数相同的平方数。这四位老师也十分尽责,第二天就拿出了他们的“研究成果”,印了一份“尾数相同的平方数表格”,印发给大家参考探讨。
尾数相同的平方数表格:
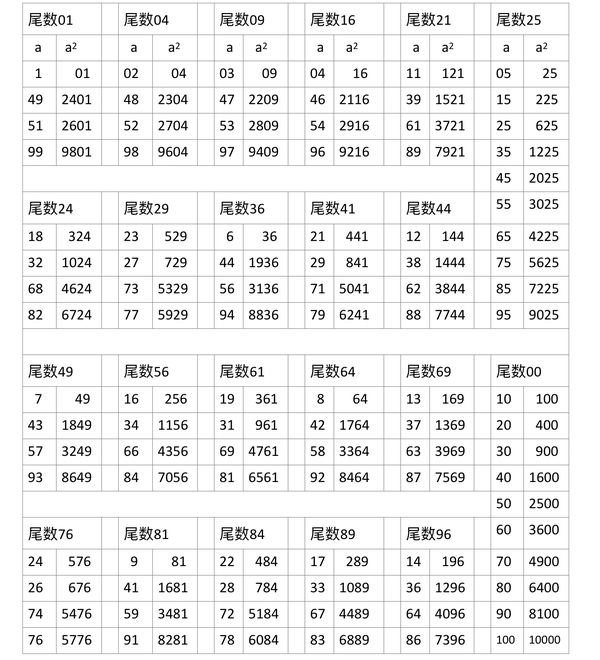
四位负责整理这平方数尾数的老师中,大家推选出一位男老师M给大家介绍这平方数尾数表的整理情况。M老师当年在本地高考中,数学一科曾得到满分,后来又在大学数学系中攻读了四年,故其数学水平高于一般老师。其的介绍如下:
正如昨天讨论时有的老师提出的那样,并不是任何一个两位数都能成为平方数的尾数的。我们在整理过程中发现,只有22个两位数能成为平方数的尾数的。这22个数分别为:01,04,09,16,21,24,25,29,36,41,44,49,56,61,64,69,76,
81,84,89,96及00。这在发给大家的表格中也可见到。
这些尾数中,25与00是较为特殊的。正如大家之前就已讨论过的那样,个位数是5的自然数,其等的平方数中最后两位数(尾数)都是25。所以1到100的自然数中,平方数尾数是25的就有10个,分别是5,15,25,35------到95。同样的,自然数中个位数如果是0的话,其平方数的尾数就是00,所以1到100的自然数中,10,20,30,40------到100这10个数的尾数都会是00。
除25及00外,其他能成为平方数尾数的两位数还有20个。整理中发现,每个尾数都拥有4个平方数。这样说也许不容易明白,或者可以这样说:1到100之内的自然数中,每4个自然数的平方数都会有一个相同的尾数。例如,1,49,51,99这四个数就有相同的尾数01;同样的,2,48,52,98这四个数的平方数有相同的尾数04;11,39,61,89这四个数的平方数中也有相同的尾数21。这些在表格中都已一个个地列出来了,大家可以仔细检查看看,有错误的地方也可以马上指出来以便更正。
那么平方数尾数相同的自然数之间互相有什么关系呢?
我个人的发现是:假使a, b, c, d (按数值从小到大排列)这四个自然数的平方数有相同的尾数之话,那么这四个数会有以下关系:a + b = 50,b + c = 100,c + d = 150,大家可以检查看看,这关系是否正确。
这有什么好处呢?就是如果我们知道一个自然数的平方数之后,很快就可以知道:还有哪些自然数的平方数会与该自然数的平方数有相同的尾数了。
例如,你已知道:232 = 529,那么就可以知道27,73,77这些数平方数的尾数也是29了。是不是这样大家可以检查看看,我的介绍就先讲到这里,其他老师也可以说出自己的看法和意见。
负责整理这平方数尾数的一位年青女老师也站起来说:“M老师 的介绍是相当全面了。不过我个人的看法是,一个自然数a,会与其他三个自然数50 – a,50 + a及
100 – a拥有相同的平方数尾数。而且我们一旦知道这自然数a的平方数,也很快就可以找出这50 – a,50 + a,100 – a这三个自然数的平方数了。”说完,就在黑板上写下了一下算式:
已知:242 = 576,则 262 – 242 = ( 26 + 24)( 26 – 24) = 50 x 2 = 100,
所以262 = 100 + 576 =676
同理,742 – 242 = ( 74 + 24 )( 74 – 24 ) = 98 x 50 = 4900
所以 742 = 4900 + 576 = 5476
762 – 242 = ( 76 + 24 )( 76 – 24) = 100 x 52 =5200
所以 762 = 5200 + 576 =5776
说到这里,大家都对这表格中的数据关系更感兴趣,纷纷对这表格仔细观察,并寻找各数据之间的关系。
评论列表 共有 0 条评论
最新导读

热门文章















发表评论 取消回复